According to the book "Social Choice and Individual Values" in every election there are 3 criteria that we can consider if it is to be 'fair':
- Unanimity: If everyone prefers one candidate over another then that candidate should be elected
- Independence of Irrelevant Alternatives: If everyone's preference between candidates A and B stay the same then that preference should not change even if people change their mind between A and another candidate C or B and C.
- Non-Dictatorship: There shouldn't be one. No single voter should posses the power to determine the outcome of the election.
By formalising the results of an election mathematically we can show that not voting systems satisfies all 3 of these criteria. This is called Arrow's Impossibility Theorem. I will be using the proof of a pivotal voter below. However, what this essentially shows is that by the introduction of an alternative candidate this can throw off the results of an election. In other words they are a spoiler candidate.
This does not outright mean that every election is unfair but rather that every election can be unfair. As Arrow said "Most [ranked] systems are not going to work badly all of the time. All I proved is that all can work badly at times".
This is a presentation form of the proof and it is written out completely below.
Written Proof
Let G be a set of outcomes, N a number of voters, and we shall denote the set of all full linear orderings of G by L(G).
We can let F be a social welfare function whereby:
$$ F : L(G)^N -> L(G) $$
which aggregates voters' preferences into a single preference order on G. An N-Tuple %% (R_1, ..., R_n) \in L(G)^N %% is called a preference profile.
Now let's formalise what each of these criteria strictly means:
Unanimity: If A is ranked strictly higher than B for every ordering %% R_1,...,R_N %% then A is ranked strictly higher than B for %% F(R_1,...,R_N) %%.
Independence of Irrelevant Alternatives: For two preference profiles %% (R_1,...,R_N) %% and %% (S_1,...,S_N) %% if every individual %% i %% ranks A and B the same in %% R_i%% as in %% S_i %% then A and B will have the same ranking in %% F(R_1,...,R_N) %% and %% F(S_1,...,S_N) %%
Non-Dictatorship: There is no individual %% i %% whose preference always prevails. In other words there is no $$ i : \forall (R_1,...,R_N) \isin L(A)^N $$ if voter %% i %% ranks A above B by %% R_i %% then this implies A will rank above B by %% F(R_1,...,R_N) %%.
Now that we have formalised what our fundamental criteria are, we can go about showing that they can't all hold. We will do this in 3 steps
- Prove that there is a "pivotal" voter for B over A
- Show that this pivotal voter for B over A is a dictator for B over C
- Show there there exists a dictator
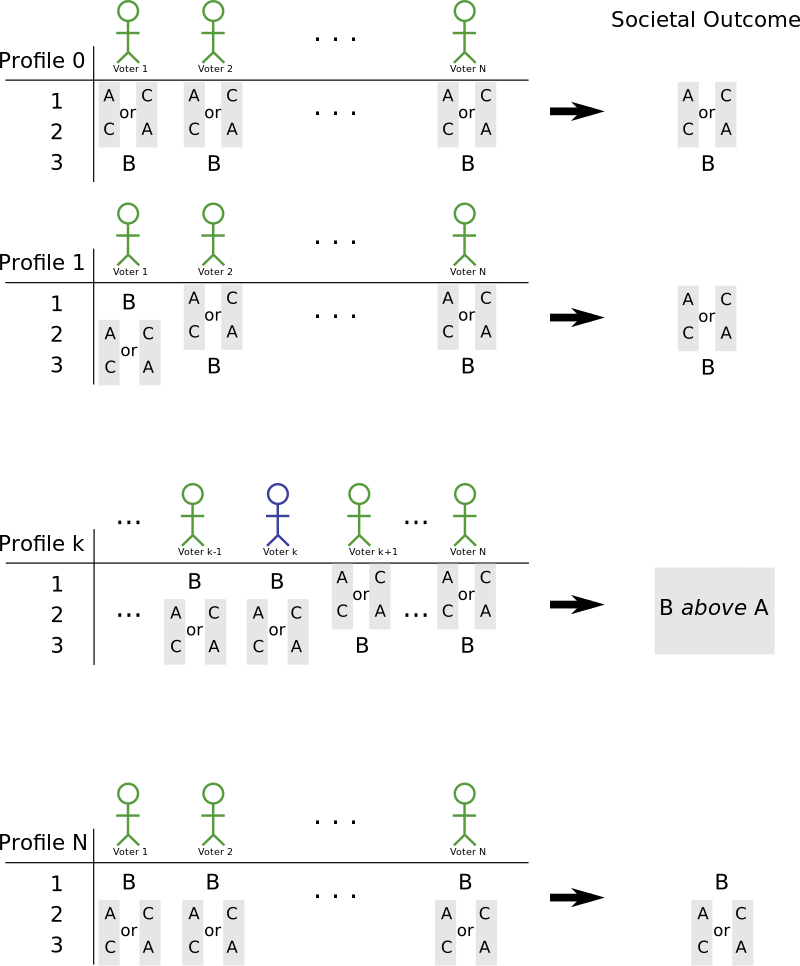
Let's imagine a scenario where there are 3 candidates (A, B, C). Everyone prefers both A to C and B to C. By our unanimity principle we can say that society prefers A and C to B. Let's refer to this as profile 0.
If we consider a different scenario where everyone preferred B to A and C then society would have to prefer B by unanimity also. We can consider changing each person's vote to have B as the first preference to gradually move from profile 0 to this new profile. For each voter i let profile i be the same as profile 0 but move B to the top of the ballot for voters 1 through i.
After a certain number of votes are cast for them B will eventually rank higher than A. The person who puts them over the line is called the "pivotal voter for B over A" and we'll refer to the profile where this happens profile k.
To prove that this pivotal voter k is also a dictator over C we must prove that it doesn't matter how everyone else voted. Let's call all voters 1 through k-1 segment 1 and voters k+1 through N segment 2. In other words all the voters who have changed their mind to B top of the ballet are in the first segment and all the voters who kept their vote are in the second segment. Now suppose:
| Segment 1 ranks | B>C>A |
| Pivotal Voter ranks | A>B>C |
| Segment 2 ranks | A>B>C |
Because our pivotal voter ranks A>B then the outcome of the election should have A>B but because every voter has ranked B higher than C then the election should also have B higher than C. This means our pivotal voter is a dictator for B over C. Now suppose instead:
| Segment 1 ranks | C>B>A |
| Pivotal Voter ranks | B>A>C |
| Segment 2 ranks | A>C>B |
In other words our pivotal voter has moved B above A above A and everyone else has moved B below C. This is the same result as in profile k except C has been changed. So, B must rank above A in the societal outcome. Furthermore A must rank above C because of our Independence of Irrelevant Alternatives principle.
So, the societal outcome will rank B>C even though our pivotal voter is the only one to rank B>C. This makes him a dictator for B over C.
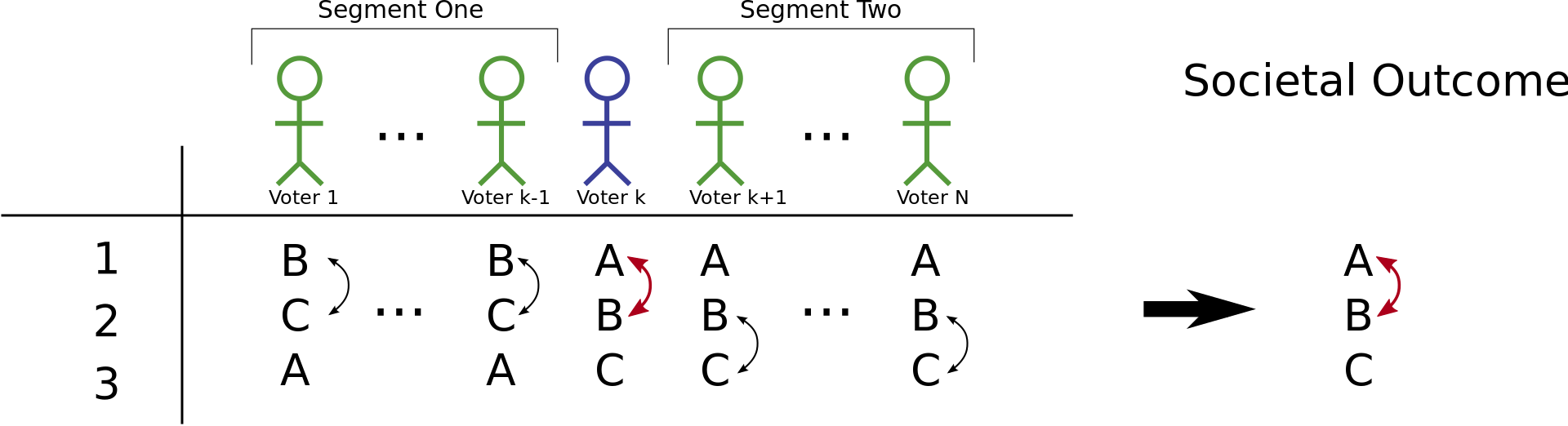
We can now apply the first 2 steps to find the pivotal voter for B over C and C over B. By moving B to the top of more ballots the pivot point where society ranks B>C must come before our dictator. Reversing this we find that the pivot point for C>B must come after the dictator. In other words:
$$ k_{\frac{B}{C}} \leq dictator \leq k_{\frac{C}{B}}$$
$$ k_{\frac{B}{C}} \leq k_{\frac{B}{A}} \leq k_{\frac{C}{B}}$$
However, B was a random choice. If we repeat this entire argument with B and C switched we also have:
$$ k_{\frac{C}{B}} \leq k_{\frac{B}{C}}$$
And so:
$$ k_{\frac{B}{C}} = k_{\frac{B}{A}} = k_{\frac{C}{B}} $$
And if we repeat this for all the different pairs of voters then we can show that this dictator is the dictator for the entire election.